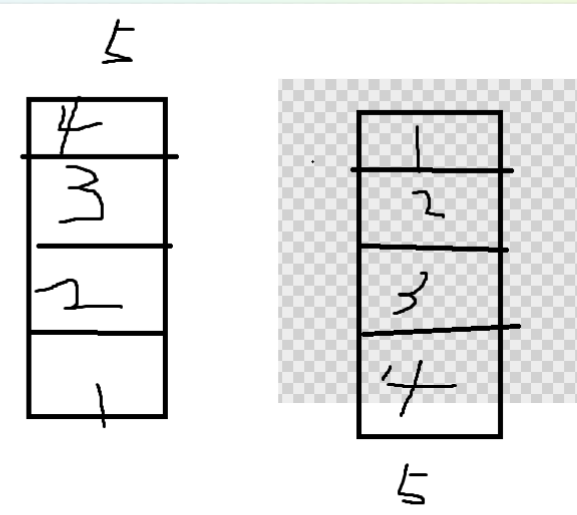
二分 排序数组找区间 题目链接:
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
我发现二分有时候还真不会,应该是自己有的地方没搞明白,做了一下还真是
这次差不多算是了解一些细节了
详细的放注释里
#include <vector> using std::vector;class Solution { public : vector<int > searchRange (vector<int >& nums, int target) { if (nums.empty ()) return vector<int >{-1 ,-1 }; int l = 0 ,r = nums.size () - 1 ; while (l < r) { int mid = ( l + r )>> 1 ; if (nums[mid] < target) l = mid + 1 ; else r = mid; } int ans1 = l; if (l == nums.size () || nums[l] != target) return vector<int >{-1 ,-1 }; else { r = nums.size (); while (l < r) { int mid = (l + r) >> 1 ; if (nums[mid] > target) r = mid; else l = mid + 1 ; } return vector<int >{ans1,l}; } } };
完全二叉树的节点个数 递归迭代也能做,但效率差一些,这次不写了,说说二分怎么做
二分做这题要搭配位运算,为什么呢
在最后一行,我们的节点个数大致范围已经确定,那个什么k-1到那个什么k的区间里取值,此时二分里的check函数要写什么呢
写的就是判断某个节点存不存在,而这就需要搭配位运算进行
例如我们要找到节点12号,他的2进制表示为1100,以1为right,0为left,去除开头的1,我们得到的就是根节点到此节点的路径
以上,我们就可以写出对应的二分答案
struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode () : val (0 ), left (nullptr ), right (nullptr ) {} TreeNode (int x) : val (x), left (nullptr ), right (nullptr ) {} TreeNode (int x, TreeNode *left, TreeNode *right) : val (x), left (left), right (right) {} }; class Solution { public : int find_Height (TreeNode* root) { int res = 0 ; while (root) { root = root->left; res++; } return res; } int count_Full_Nodes (int height) { int res = 0 ; for (int i = 0 ;i < height;++i) { res += pow (2 ,i); } return res; } bool check_Node (TreeNode* root,int index) { vector<int > nums; while (index) { nums.push_back (index % 2 ); index /= 2 ; } nums.pop_back (); std::reverse (nums.begin (),nums.end ()); for (auto t : nums) { if (t) root = root->right; else root = root->left; } return root; } int countNodes (TreeNode* root) int h = find_Height (root); int l = count_Full_Nodes (h-1 ); int r = count_Full_Nodes (h); while (l < r) { int mid = (l + r + 1 ) >> 1 ; if (check_Node (root,mid)) l = mid; else r = mid - 1 ; } return l; } };
链表 两数相加 https://leetcode.cn/problems/add-two-numbers/
解题思路: 大数相加思想,链表递进
struct ListNode { int val; ListNode *next; ListNode () : val (0 ), next (nullptr ) {} ListNode (int x) : val (x), next (nullptr ) {} ListNode (int x, ListNode *next) : val (x), next (next) {} }; class Solution { public : ListNode* addTwoNumbers (ListNode* l1, ListNode* l2) { ListNode* res = new ListNode (); ListNode* tmp = res; int add = 0 ; while (l1 || l2 || add) { int sum = 0 ; if (l1) sum += (*l1).val; if (l2) sum += (*l2).val; sum += add; add = sum / 10 ; (*tmp).val = sum % 10 ; if (l1) l1 = (*l1).next; if (l2) l2 = (*l2).next; ListNode* next = new ListNode (); (*tmp).next = next; tmp = (*tmp).next; } for (ListNode* i = res;i != nullptr ;i = (*i).next) { ListNode* next = (*i).next; if ((*next).val == 0 && (*next).next == nullptr ) (*i).next = nullptr ; } return res; } };
队列 用栈实现队列 https://leetcode.cn/problems/implement-queue-using-stacks/?envType=daily-question&envId=2024-03-04
关键在于如何灵活运用好两个栈,由于进阶说明中提到:即使其中一个操作可能花费较长时间,可以推断出就是push操作进行一番推理,pop,top应该是O(1)复杂度
3ms写法 push操作推理如下:
我们认为q2中元素已经有多个,且q2就是我们pop等操作所使用的栈,我们可以试着将q2元素逆序放到q1中
假设q2还存在,此时想要将新push的元素放到q2栈底中
将新元素放进q1中,再逆序放回q2
此时的q2就是push后新形成的伪队列
#include <stack> using std::stack;class MyQueue { public : MyQueue () { stack<int >* s1 = new stack <int >(); stack<int >* s2 = new stack <int >(); q1 = s1; q2 = s2; } void push (int x) int sz = q2->size (); for (int i = 0 ;i < sz;++i) { q1->push (q2->top ()); q2->pop (); } q1->push (x); sz++; for (int i = 0 ;i < sz;++i) { q2->push (q1->top ()); q1->pop (); } } int pop () int res = q2->top (); q2->pop (); return res; } int peek () return q2->top (); } bool empty () if (q2->empty ()) return true ; else return false ; } private : stack<int >* q1; stack<int >* q2; };
0ms写法 原理类似上面的,不解释了
#include <stack> using std::stack;class MyQueue { public : MyQueue () { stack<int >* s1 = new stack <int >(); stack<int >* s2 = new stack <int >(); q1 = s1; q2 = s2; } void push (int x) q1->push (x); } int pop () swap (); int res = q2->top (); q2->pop (); return res; } int peek () swap (); int res = q2->top (); return res; } void swap () { if (q2->empty ()) { while (!q1->empty ()) { q2->push (q1->top ()); q1->pop (); } } } bool empty () return q1->empty () && q2->empty (); } private : stack<int >* q1; stack<int >* q2; };
dfs区 [NOIP2001 普及组] 求先序排列 题目描述 给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,且二叉树的节点个数 $ \le 8$)。
输入格式 共两行,均为大写字母组成的字符串,表示一棵二叉树的中序与后序排列。
输出格式 共一行一个字符串,表示一棵二叉树的先序。
样例 #1 样例输入 #1 样例输出 #1 提示 【题目来源】
NOIP 2001 普及组第三题
提交 #include <iostream> using std::cout;using std::endl;using std::string;void solve (string inorder,string postorder) if (inorder.length () > 0 ) { char ch = postorder[postorder.length ()-1 ]; cout<<ch; int k = inorder.find (ch); solve (inorder.substr (0 ,k),postorder.substr (0 ,k)); solve (inorder.substr (k+1 ),postorder.substr (k,inorder.length () -(k +1 ))); } } int main () string inorder,postorder; std::cin >> inorder >> postorder; solve (inorder,postorder); return 0 ; }
二叉树的中序遍历 https://leetcode.cn/problems/binary-tree-inorder-traversal/
递归很简单,但迭代法我觉得应该往中等靠靠
递归法
#include <vector> #include <stack> using std::vector;using std::stack;struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode () : val (0 ), left (nullptr ), right (nullptr ) {} TreeNode (int x) : val (x), left (nullptr ), right (nullptr ) {} TreeNode (int x, TreeNode *left, TreeNode *right) : val (x), left (left), right (right) {} }; class Solution { public : vector<int > inorderTraversal (TreeNode* root) { vector<int > res; vector<int > left; vector<int > right; vector<int > in; if (root->left) left = inorderTraversal (root->left); if (root) in.push_back (root->val); if (root->right) right = inorderTraversal (root->right); if (!left.empty ()) res.insert (res.end (),left.begin (),left.end ()); if (!in.empty ()) res.insert (res.end (),in.begin (),in.end ()); if (!right.empty ()) res.insert (res.end (),right.begin (),right.end ()); return res; } };
迭代法
class Solution { public : vector<int > inorderTraversal (TreeNode* root) { vector<int > res; stack<TreeNode*> st; TreeNode* cur = root; while (cur || !st.empty ()) { if (cur) { st.push (cur); cur = cur->left; } else { cur = st.top (); st.pop (); res.push_back (cur->val); cur = cur->right; } } return res; } };
二叉搜索树 https://leetcode.cn/problems/validate-binary-search-tree/
没听说过,所以学学
二叉搜索树概念 二叉搜索树(BST,Binary Search Tree),也称二叉排序树 或二叉查找树。
非空左子树的所有键值小于其根结点的键值。
非空右子树的所有键值大于其根结点的键值。
左、右子树都是二叉搜索树。
查找操作:
(1)查找从根结点开始,如果树为空,返回NULL
尾递归查找:
typedef int ElementType;typedef struct TNode *Position;typedef Position BinTree; struct TNode { ElementType Data; BinTree Left; BinTree Right; }; Position Find (ElementType X,BinTree BST) if (!BST) return nullptr ; else if (X > BST->Data) return Find (X,BST->Right); else if (X < BST->Data) return Find (X,BST->Left); else return BST; }
迭代法查找
Position Find (ElementType X,BinTree BST) while (BST) { if (X > BST->Data) BST = BST->Right; else if (X < BST->Data) BST = BST->Left; else return BST; } return nullptr ; }
查找最大最小元素 ①最大元素一定是在树的最右分枝的端结点上。
因此可以通过查找左树里查找没有左节点只有右树的节点查找最小值
同理找最大值,他们两个都是唯一的
Position FindMin (BinTree BST) if (BST) { while (BST->Left) BST = BST->Left; return BST; } }
搜索树插入 二叉搜索树在插入前,肯定要找到插入的位置。所以解决这个问题的关键就是要找到元素应该插入的位置,可以采用与Find类似的方法。
Position insert (ElementType X,BinTree BST) if (!BST) { BST = (BinTree)malloc (sizeof (struct TreeNode)); BST->Data = X; BST->Left = BST->Right = nullptr ; } else { while (BST) { if (X > BST->Data) BST->Right = insert (X,BST->Right); else if (X < BST->Data) BST->Left = insert (X,BST->Left); } } return BST; }
搜索树删除 对于二叉搜索树的删除,相对来说就比较麻烦了。因为要考虑以下三种情况:
情况①: 删除之后要修改其父结点指针,即置为NULL。
情况②:
情况③:
值得注意的是:当我们找到元素替代被删除的结点后,我们也要删除用来替代元素。删除该元素的方法也是按照以上3种情况分析
Position FindMin (BinTree) ;BinTree Delete (ElementType X,BinTree BST) Position Tmp; if (!BST) { return nullptr ; } else { if (X < BST->Data) BST->Left = Delete (X,BST->Left); else if (X > BST->Data) BST->Right = Delete (X,BST->Right); else { if (BST->Left && BST->Right) { Tmp = FindMin (BST->Right); BST->Data = Tmp->Data; BST->Right = Delete (BST->Data,BST->Right); } else { Tmp = BST; if (!BST->Left) BST = BST->Right; else BST = BST->Left; free (Tmp); } } } return BST; }
题目
https://leetcode.cn/problems/validate-binary-search-tree/
做完发现和二叉搜索树应用没啥联系
关键点在于理解搜索二叉树左小右大.因此我们可以通过中序遍历得到一串升序数组,判断数组里是否有降序即可
#include <stack> #include <cstdlib> #include <vector> using std::stack;using std::vector;struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode () : val (0 ), left (nullptr ), right (nullptr ) {} TreeNode (int x) : val (x), left (nullptr ), right (nullptr ) {} TreeNode (int x, TreeNode *left, TreeNode *right) : val (x), left (left), right (right) {} }; class Solution {public : bool isValidBST (TreeNode* root) stack<TreeNode*> st; vector<long long > arr; TreeNode* cur = root; while (cur || !st.empty ()) { if (cur) { st.push (cur); cur = cur->left; } else { cur = st.top (); arr.push_back (cur->val); st.pop (); cur = cur->right; } } int sz = arr.size (); for (int i = 1 ;i < sz;++i) { if (arr[i] < arr[i-1 ] || arr[i] == arr[i-1 ]) return false ; } return true ; } };
恢复二叉搜索树 99. 恢复二叉搜索树 - 力扣(LeetCode)
也是因为中序遍历后得到的升序数组有问题,和排序后的进行比较,找到不同的两者进行交换即可
#include <stack> #include <vector> #include <algorithm> #include <iostream> #include <map> using std::stack;using std::vector;using std::map;struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode () : val (0 ), left (nullptr ), right (nullptr ) {} TreeNode (int x) : val (x), left (nullptr ), right (nullptr ) {} TreeNode (int x, TreeNode *left, TreeNode *right) : val (x), left (left), right (right) {} }; class Solution { public : void recoverTree (TreeNode* root) stack<TreeNode*> st; vector<int > arr; TreeNode* cur = root; map<int ,TreeNode*> m; while (cur || !st.empty ()) { if (cur) { st.push (cur); cur = cur->left; } else { cur = st.top (); arr.push_back (cur->val); m[cur->val] = cur; st.pop (); cur = cur->right; } } vector<int > arr2 = arr; std::sort (arr.begin (), arr.end ()); int dif[2 ] = {0 }; int index = 0 ; int sz = arr.size (); for (int i = 0 ;i < sz;++i) { if (arr[i] != arr2[i]) dif[index++] = arr[i]; } int tmp = 0 ; tmp = m[dif[0 ]]->val; m[dif[0 ]]->val = m[dif[1 ]]->val; m[dif[1 ]]->val = tmp; } };
对称二叉树,相同二叉树 一开始我是不会的,但是看了代码随想录的题解,哇,原来还能这么遍历,因此我要把这两题加进来,他们的原理是差不多的,对称二叉树是内外比较,相同二叉树就是普通的比较
题目链接
101. 对称二叉树 - 力扣(LeetCode)
将根节点左右子树看成两个单独的树,分割开来,从根节点开始比较
根节点的多种情况比较完之后,将两棵树外侧根节点加入到递归,栈,队列当中(下一次比较的就是外侧根节点),接着比较内侧根节点
如此往复形成了递归或者迭代
struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode () : val (0 ), left (nullptr ), right (nullptr ) {} TreeNode (int x) : val (x), left (nullptr ), right (nullptr ) {} TreeNode (int x, TreeNode *left, TreeNode *right) : val (x), left (left), right (right) {} }; class Solution { public : bool compare (TreeNode* left,TreeNode* right) { if (!left && !right) return true ; else if (!left || !right) return false ; else if (left->val != right->val) return false ; else { bool outside = compare (left->left,right->right); bool inside = compare (left->right,right->left); return outside && inside; } } bool isSymmetric (TreeNode* root) return compare (root->left,root->right); } };
迭代(队列)(队列和栈写法一样,都是两两取出来比较)
class Solution { public : bool compare (TreeNode* left,TreeNode* right) { queue<TreeNode*> q; q.push (left); q.push (right); while (!q.empty ()) { TreeNode* r = q.front (); q.pop (); TreeNode* l = q.front (); q.pop (); if (!l && !r) continue ; else if (!l || !r) return false ; else if (l->val != r->val) return false ; else { q.push (l->left); q.push (r->right); q.push (l->right); q.push (r->left); } } return true ; } bool isSymmetric (TreeNode* root) return compare (root->left,root->right); } };
100. 相同的树 - 力扣(LeetCode)
原理和对称二叉树是一样的,这次比较的同样是两棵树,但是是按照正常的左右遍历来
class Solution { public : bool isSameTree (TreeNode* p, TreeNode* q) if (!p && !q) return true ; else if (!p || !q) return false ; else if (p->val != q->val) return false ; else { bool left = isSameTree (p->left,q->left); bool right = isSameTree (p->right,q->right); return left && right; } } };
class Solution { public : bool isSameTree (TreeNode* p, TreeNode* q) { if (p == nullptr || q == nullptr ) return true ; if (p == nullptr || q == nullptr ) return false ; stack<TreeNode*> st; st.push (p); st.push (q); while (!st.empty ()) { TreeNode* left = st.top (); st.pop (); TreeNode* right = st.top (); st.pop (); if (!left && !right) { continue ; } if (!left || !right || (left->val != right->val)) return false ; st.push (left->left); st.push (right->left); st.push (left->right); st.push (right->right); } return true ; } };
动态规划 动态规划和记忆化搜索可以相互转换,在做动态规划时可以试着转换成记忆化搜索解答,同样的记忆化搜索也可以转换成动态规划解决
关键点在于: 如何把一个问题分解为多个子问题(x)
真正的关键 ,true point is ,动规五部曲
没有动规五部曲,你就度过了一个失败的人生,这里有一个非常棒的讲解动规五部曲的详细教程
请看:代码随想录 (programmercarl.com)
看完之后,请随我复习一遍
动规五部曲步骤:
1.确定dp定义,写出dp数组
2.确定递推公式,状态转移方程
3.初始化数组
4.确定遍历顺序
5.推导dp数组,打印确认是否有误
下面一题是初期按照第一法得来的,可以不看,再下一页我会用动规五部曲解释
279. 完全平方数 - 力扣(LeetCode)
例如此题: 该问题是如何得到方案数最小的完全平方数和方案,我们可以设想一下答案的上一次是什么情况
例如13,他的上一个数必定是由一个数加一个平方数得到的
因此我们可以通过减去这个平方数得到上一个数,得到上一个数的方案数
依次类推就是分解为了多个子问题,从最小不能再小的子问题1开始计算,
得到最终大问题的答案
#include <vector> #include <cstring> #include <iostream> #include <algorithm> using std::cout;using std::endl;using std::vector;const int N = 1e4 + 1 ;class Solution { public : int numSquares (int n) int dp[N]; for (int i = 1 ;i <= n;++i) { int min = INT_MAX; for (int j = 1 ;j * j <= i;++j) { min = std::min (min,dp[i - j*j]); } dp[i] = min + 1 ; } return dp[n]; } };
一维dp,普通dp 完全平方数 279. 完全平方数 - 力扣(LeetCode)
轻易得知,dp数组存的一定是当前下标i对应的完全平方数的最少数量
让我们随机挑一个数,例如59,我们可以在此基础上减去一个平方数,
例如59-4 = 55,假设我们已经算出来了55的最少完全平方数(实际运算到59时也是已知的),那么dp[59] = std::min(dp[59],dp[55] + 1)(关键最少所以选min)
推出状态转移方程为dp[i] = std::min(dp[i],dp[i-j * j] + 1);//j从0-i中选,且j*j <= i;
得到了递推关系式,我们也就能根据此来进行初始化
我们现在需要初始化的仅有dp[0],让其 = 0, 此时我们算得的dp[1] = 1,dp[4] = 1,等等
遍历顺序0-i,j-i
推导方程,检验
class Solution { public : int numSquares (int n) vector<int > dp (n + 1 ) ; dp[0 ] = 0 ; for (int i = 1 ;i <= n;++i) { dp[i] = INT_MAX; for (int j = 1 ;j * j <= i;++j) { dp[i] = std::min (dp[i],dp[i- j * j] + 1 ); } } return dp[n]; } };
斐波那契 dp入门,斐波那契数列 509. 斐波那契数 - 力扣(LeetCode)
dp的入门必做一题,想必大家都会了
现在我们用五部曲的思路顺一遍
定义dp数组
显而易见,dp根据下标i存储对应的斐波那契数
递推公式
这个题目已经告诉你了,也是为什么这道题如此简单的原因
dp[i] = dp[i-1] + dp[i-2];
初始化数组
首先我们根据递推公式,每次计算都需要前两个数的状态,那么初始化必定需要初始化0和1
遍历顺序应当从2开始,0和1都无法使用这条递推公式
检验一遍,并考虑到n == 0时,初始化1无法进行,因为发生了数组越界,
因此我们可以在n == 0时直接返回结果
class Solution { public : int fib (int n) if (n == 0 ) return 0 ; vector<int > dp (n + 1 ) ; dp[0 ] = 0 ; dp[1 ] = 1 ; for (int i = 2 ;i <= n;++i) dp[i] = dp[i-1 ] + dp[i-2 ]; return dp[n]; } };
最小花费 746. 使用最小花费爬楼梯 - 力扣(LeetCode)
这一次是入门状态转移的经典,我们通过之前的状态来得到当前状态的最佳方案
确定dp数组
dp[i]表示的就是在到达i阶楼梯时的最小花费
dp[i] = std::min(dp[i-1] + cost[i-1],dp[i-2] + cost[i-2])
根据题意很容易得出来
初始化dp[0] = 0,dp[1] = 0,因为我们每次更新dp都需要前两次状态,且我们可以选择从0或者从1出发
从前到后遍历
检验没有其余特殊情况
class Solution {public : int minCostClimbingStairs (vector<int >& cost) vector<int > dp (cost.size() + 1 ) ; dp[0 ] = 0 ; dp[1 ] = 0 ; for (int i= 2 ;i <= cost.size ();++i) { dp[i] = min (dp[i-1 ] + cost[i-1 ],dp[i-2 ] + cost[i-2 ]); } return dp[cost.size ()]; } };