基础算法

排序

1. 快排

​ 确定一组数据 ，即q数组

​ 左端点为l，右端点为r

​ （1）确定分界点

​ q[l] 或 q[ (l + r) / 2] 或 q[r] 或任意一个数 作为分界点，分界点数为x

​ （2）调整区间 （重点）

​ 使 <= x的数放在左半边，使 >= x 的数放在右半边，两边的数可以乱序，暂时不用排序

​ （3）利用递归处理左右两端 ，进行排序

​ 暴力法

​ （1）开两个额外数组a，b

​ （2）扫描 l 到 r 的所有数，将 <= x 的值放到a中，将 >= x的数放到b中

​ （3）将a，b排序后放到q数组中 a[ ] -> q[ ], b[ ]->q[ ];

​ （4）弊端：额外开辟空间，占用内存

​ 简便方法（指针）

​ 用两个指针i，j指向左端与右端的数

​ （1）判断指针i所指向的数是否小于x，符合条件时往右移一位，当大于等于x时指针i停下

​ （2）判断指针j所指向的数是否大于x，符合条件时往左移一位，当小于等于x时指针停下

​ （3）将i与j指针所指向的数交换，并再次重复1，2，3，直到i，j走到中间位置

​ （4）两边排序

模板

#include <iostream> // scanf和printf也在iostream里面 ，但cstdio更快一些
#include <cstdio> 
#include <algorithm> //使用swap函数
using namespace std;
const int N = 1000001;

int n;
int q[N];

void quick_sort(int q[ ], int l, int r)
{
	if (l >= r) return ; // 返回一个随机值，该return只是起到一个中止的作用，无需返回特定值

	int x = q[l], i = l - 1, j = r + 1,;
    //x = q[(l+r+1 )/2	一定不能取到边界上，上面的x只是举例
    // x = q[l + r >> 1]会更快,以后再理解
	while (i < j)
	{
		do {
			i++;
		} while (q[i] < x);
		
		do {
			j--;
		} while (q[j] > x);

			if (i < j) swap(q[i],q[j]);
	}

	if(l < j )quick_sort(q, l, j);//左半部分
	if(i < r)quick_sort(q, j + 1, r);//右半部分

}
int main()
{
	scanf("%d", &n);
	for (int i = 0;i < n;++i) scanf("%d", &q[i]);

	quick_sort(q, 0, n-1);

	for (int i = 0;i < n;++i) printf("%d ", q[i]);

	return 0;
}

2. 归并排序

​ (方法和快排类似，但顺序不同)

​ 有一组数据q[ ]

​ (1) 以数组中间作为分界点

​ （2）将两边利用递归排序

​ （3）归并，将两个数组合二为一（重点）

模板

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstdio>
using namespace std;

const int N = 100010;
int n;

int q[N];
int tmp[N];
void merge_sort(int q[], int l, int r)
{
	if (l >= r) return;
	//确定分界点
	int mid = (l + r) >> 1;// (l+r)/2
	//分成两边
	merge_sort(q, l, mid);
	merge_sort(q, mid+1, r);
	//归并 合二为一
	int k = 0, i = l, j = mid + 1;
	while (i <= mid && j <= r)
	{
		if (q[i] <= q[j] ) tmp[k++] = q[i++];
		else tmp[k++] = q[j++];
	}
	//两边如果有元素未遍历
	while (i <= mid) tmp[k++] = q[i++];
	while (j <= r) tmp[k++] = q[j++];

	//把tmp赋给q
	for (int i = l, j = 0;i <= r;i++, j++) q[i] = tmp[j];
}
int main()
{
	scanf("%d", &n);

	for (int i = 0;i < n;++i) scanf("%d", &q[i]);

	merge_sort(q, 0, n - 1);

	for (int i = 0;i < n;++i) printf("%d ", q[i]);

	return 0;
}

时间复杂度

​ 快排的平均时间复杂度为 n * n，归并的时间复杂度为 n * log n 且log 以2为底，因为快排存在递归，所耗时间多，归并每个数据只移动一次，时间是线性的

二分

二分的本质

如果有单调性一定可以二分，但是可以二分的题目不一定非得有单调性（没有单调性，也有可能可以二分），二分的本质并不是单调性，单调性和二分没有直接的关系

单调性：如果想找一个中间值的话，如果这个点小的话，答案一定在右半边，这个点如果大的话，答案一定在左半边

二分的本质是边界：

1. 整数二分

​ （1） 找到中间值

​ 模板1（分左半边区域）：mid = （ l + r + 1 ）/2，并判断该中间值是否满足性质，check该值是否属于左半边区域，如果满足，则一定在左半边区域,如果不满足，则在右半边区域，又继续判断新的mid值是否满足性质，以此类推

//区间[l,r]被划分成[l,mid - 1]和 [mid,r]时使用
int bsearch_1(int l,int r)
{
	while(l < r) //直到找出最小下标范围[l,r];
	{
		int mid = l + r + 1 >> 1;
		if(	check(mid) ) l = mid;//check判断是否满足性质
		else r = mid - 1;
	}
     return l;
}

​ 目的：在升序，无重复元素的数组中寻找特定值的下标

​ 模板2（分右半边区域）：mid = （l + r）/2，并判断该数是否满足规律，如果不满足，则让 ,r= mid,如果不满足，则让l = mid + 1

//区间[l,r]被划分成[l,mid]和[mid + 1,r]时使用
int bsearch_2(int l ,int r)
{
    while(l < r)
    {
        int mid = l + r >> 1;
        if(chech(mid)) r= mid;
        else l = mid + 1;
    }
    return l;
}

选择哪个模板，重点在于看下一次区间更新是l = mid，还是r = mid

如果是前者，mid则需要补1，如果是后者，则不需要补1

补1的原因：如果l = mid ，由于整数除法是下取整，有可能l 会一直等于mid，r一直不变，l，r不再更新，形成死循环

2. 浮点数二分

​ 基本和整数二分类似，但无需考虑边界问题，是否会形成死循环

高精度

​ 位数最大为1e6(10 的6 次方)

​ 加减乘除四种存储方式是相同的

1.高精度加法

​ 思想：分别用两个数组逆存储两个整数的值，数组下标为0的值存储个位，为1存在十位，以此类推；

​ 再通过模拟加法进位来将得到的值的每一位存储的新数组当中，得到相加数

模板

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
#include <string>

using namespace std;

const int N = 1000010;

vector<int> add(vector<int> &A, vector<int> &B)//传址调用，节省占用，无需再另拷贝新数组
{
	vector<int> C;
	int t = 0;
	for (int i = 0;i < A.size() || i < B.size();++i)
	{
		if (i < A.size()) t += A[i];
		if (i < B.size()) t += B[i];
		C.push_back(t % 10);
		t /= 10;
	}
	if (t) C.push_back(1);
	return C;
}
int main()
{
	string a, b;
	vector <int> A, B;
	cin >> a >> b;// a = "123456"
	for (int i = a.size( )-1;i >= 0;--i) A.push_back(a[i] - '0');//{6,5,4,3,2,1}
	for (int i = b.size( )-1;i >= 0;--i) B.push_back(b[i] - '0');

	auto C = add(A, B);

	for (int i = C.size() - 1;i >= 0;--i)
	{
		cout << C[i];
	}
	
	return 0;
}

2.高精度减法

​ 思想：分别用两个数组逆存储两个整数的值，数组下标为0的值存储个位，为1存在十位，以此类推；

​ 提前判断A，B的谁大谁小，使得最终能够大数减小数，如果是B-A，还要提前打印一个负号

​ 再通过模拟减法运算，将得到的值的每一位存储的新数组当中，得到相减数，最后注意前导0的存在

模板

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
using namespace std;
bool cmp(vector<int>& A, vector<int>& B)//判断A是否大于等于B
{
	if (A.size() != B.size()) return A.size() > B.size();
	for (int i = A.size() - 1;i >= 0;--i)
	{
		if (A[i] != B[i]) return A[i]>B[i];
	}
	return true;
}
vector<int> Sub(vector<int>& A, vector<int>& B)
{
	vector<int> C;
	int t = 0;
	for (int i = 0;i < A.size();++i)
	{
		t = A[i] - t;
		if (i < B.size()) t -= B[i];// 检测B是否越界
		C.push_back((t + 10) % 10);//t为正数与t为负数两种情况判断
        // 比如7-8 是负数，模拟减法后则为10+7-8，之后也要后面一位减1
		if (t < 0) t = 1;
		else t = 0;
	}
	while (C.size() > 1 && C.back() == 0) C.pop_back(); //防止前导0的存在，需要去0
	return C;
}
int main()
{
	string a, b;
	vector<int> A, B;
	cin >> a >> b;
	for (int i = a.size() - 1;i >= 0;--i) A.push_back(a[i] - '0');
	for (int i = b.size() - 1;i >= 0;--i) B.push_back(b[i] - '0');
	if (cmp(A, B))
	{
		auto C = Sub(A, B);
		for (int i = C.size() - 1;i >= 0;--i) cout << C[i];
	}
	else
	{
		auto C = Sub(B, A);
		cout << '-';
		for (int i = C.size() - 1;i >= 0;--i) cout << C[i];
	}
	
	return 0;
}

3.高精度相乘 （大整数x小整数）

​ 思想：用一个数组逆存储一个整数的值，数组下标为0的值存储个位，为1存在十位，以此类推；用int 存储一个较小数

​ 通过将大数每一位的值与B相乘，并且每次运算只把算得的个位传给C，下一次将上次除去个位的数加上这一次相乘的值，最后将留下来的未能放进C的数再放进C中，得到最终的相乘数

模板

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <string>
#include <vector>

using namespace std;

vector<int> Mul(vector<int> &A, int &b)
{
	int t = 0;
	vector<int> C;
	for (int i = 0;i < A.size();++i)
	{
		t += A[i] * b;
		C.push_back(t % 10);//只往C中传个位数，其余位数暂时保留
		t /= 10;
	}
	while (t)//排除前导0
	{
		C.push_back(t % 10);
			t /= 10;
	}
	return C;
}
int main()
{
	string a;
	vector<int> A;
	int b;
	cin >> a>>b;
	for (int i = a.size()-1;i >= 0;--i) A.push_back(a[i] - '0');

	auto C = Mul(A, b);

	for (int i = C.size()-1;i >= 0;--i) cout << C[i];
	return 0;
}

4.高精度相除（大整数/小整数）

​ 思想：用一个数组逆存储一个整数的值，数组下标为0的值存储个位，为1存在十位，以此类推；用int 存储一个较小数

​ 和之前一样，但这次是从高位到低位，目的是模拟除法。并通过每次的余数来推演下一次的运算，比如算1234/11，第一位得到的余数r是1，

然后通过将余数r*10+下一位的数，得到12，12/11得到余数1，以此类推，最后得到的就是两数之商，同时也可得到最终的余数

模板

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
#include <string>

using namespace std;
vector<int> Div(vector<int> &A, int &b, int &r)
{
	vector<int> C;
	r = 0;
	for (int i = A.size() - 1;i >= 0;--i)
	{
		r = r * 10 + A[i];//上一次的余数*10+这一次要除的数，模拟除法
		C.push_back(r / b);//每一位的商
		r %= b;//余数
	}
	reverse(C.begin(), C.end());//得到的商是正过来的，而我们想要倒着输出，因此就要让商再倒过来
	while (C.size() > 1 && C.back() == 0) C.pop_back();//排除前导0
	return C;
}
int main()
{
	string a;
	int b;
	vector<int> A;
	cin >> a >> b;
	for (int i = a.size() - 1;i >= 0;--i) A.push_back(a[i] - '0');
	int r;
	auto C = Div(A, b,r);

	for (int i = C.size() - 1;i >= 0;--i) cout << C[i];//商
	cout << endl;
	cout << r;//余数
	return 0;
}

前缀和

一维前缀和

​ 思想：假设有原数组a1，a2，a3….an;

​ 求前缀和si

​ 则si = a1 + a2 + … + ai;

​ 若要求区间[l,r]之间的前缀和，则只需将r的前缀和减去l - 1的前缀和即可

​ 时间复杂度为O（1）；

模板

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstdio>

using namespace std;

const int  N = 100010;

int q[N];
int s[N];
int main()
{
	int n,m;
	scanf("%d %d", &n,&m);

	for (int i = 1;i <= n;++i) scanf("%d", &q[i]);
//每项前缀和的初始化
    for (int i = 1;i <= n;++i) s[i] = s[i - 1] + q[i];

	while (m--)
	{
		int l, r;
		scanf("%d %d", &l, &r);
		printf("%d\n", s[r] - s[l-1]);
	}
	return 0;
}

二维前缀和

​ 思想：有一二维数组q，将其看作一个长方形，其二维前缀和s[ i ] [ j ]就是从a[0] [0] 至 a [i] [j] 所有元素的和，

​ 如果想要快速得到每一个s[ i ] [ j ],可以用公式推得

​ s[i] [j] = s[i - 1] [j] + s[i] [j - 1] - s[i - 1] [j - 1] + a[i] [j];

​ 如果想要求出特定长方形x1，y1至x2，y2的长方形前缀和

​ 则可以利用公式

​ sum = s[x2] [y2] - s[x1 - 1] [y2] - s[x2] [y1 - 1] + s[x1 - 1] [y1 - 1]

模板

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

const int N = 10010;

int q[N][N];
int s[N][N];

int main()
{
	int n, m,k;
	scanf("%d%d%d", &m, &n, &k);
	
	for (int i = 1;i <= m;++i)
	{
		for (int j = 1;j <= n;++j)
			scanf("%d", &q[i][j]);
	}
	//每一项前缀和初始化
	for (int i = 1;i <= m;++i)
		for (int j = 1;j <= n;++j)
			s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i-1][j-1]+q[i][j];
	//询问
	while (k--)
	{
		int x1, y1, x2, y2;
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		//求前缀和
		printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
	}
	return 0;
}

差分

一维差分

本质

​ 前缀和的逆运算

原理

​ 有一数组a，b，使得 ai = b1 + b2 + b3 + … + bi

​ 例如 b1 = a1

​ b2 = a2 - a1；

​ b3 = a3-a2

​ bn = an-a（n-1）；

​ b就称为a的差分，a就称为b的前缀和

​ 使某一区域的前缀和被同步改变，

​ 本质上是改变边界的值，使得中间连续值得以被间接改变

​ 用处：且比原先（n）的时间复杂度优化为O（1）

例题模板

//改变a任意区间的前缀和，使该区间的前缀和+c，其他保持不变
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstdio>

using namespace std;

const int N = 10001;

int n, m;
int a[N];
int b[N];
//改变两边的值，使得中间连续值得以被间接改变，降低时间复杂度
void insert(int l, int r, int c)
{
	b[l] += c;
	b[r + 1] -= c;
}
int main()
{
	scanf("%d%d", &n, &m);
//获取前缀和即a数组
	for (int i = 1;i <= n;++i) scanf("%d", &a[i]);
//将前缀和赋给b，向b数组插入元素，假设前缀和皆为0
	for (int i = 1;i <= n;++i) insert(i, i, a[i])；
//改变区间内的前缀和
	while (m--)
	{
		int l, r, c;
		scanf("%d%d%d", &l, & r, &c);
		insert(l, r, c);
	}

	for (int i = 1;i <= n;++i) b[i] += b[i - 1];
	for (int i = 1;i <= n;++i) printf("%d ", b[i]);

	return 0;
}

二维差分

本质

​ 与一维差分相同，也是前缀和的逆运算

原理

​ 假设要改变存储前缀和的二维数组中特定矩阵发生改变

​ 则使存储前缀和的二维数组某一坐标的右下角全部改变，并使多余部分减掉，由于需改变矩阵的右下角的矩阵被减掉两次，还需要使其重新加回来，成为原本的前缀和，从而得到一个存储前缀和的矩阵中特定的小矩阵发生改变

用处

​ 降低原先笨方法的时间复杂度

模板

//改变二维前缀和中的特定矩阵元素
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstdio>
const int N = 1001;

int n, m, q;
int a[N][N];
int b[N][N];
using namespace std;
//能使大矩阵中的特定矩阵发生改变
//如果端点处改变，其右下角的所有元素都会被间接改变
void insert(int x1, int y1, int x2, int y2, int c)
{
	//实现矩阵内的控制小矩阵元素
	b[x1][y1] += c;
	b[x2 + 1][y1] -= c;
	b[x2][y1 + 1] -= c;
	b[x2 + 1][y2 + 1] += c;
}
int main()
{
	scanf("%d%d", &n, &m, &q);
	//读入数据,获取前缀和即a数组
	for (int i = 1;i <= n;++i)
		for (int j = 1;j <= m;++j)
			scanf("%d", &a[i][j]);
	//初始化b数组
	for (int i = 1;i <= n;++i)
	{
		for (int j = 1;j <= m;++j)
			insert(i, j, i, j, a[i][j]);
	}
	while (q--)
	{
		int x1, y1, x2, y2,c;
		//控制特定矩阵的元素
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2,&c);
		insert(x1, y1, x2, y2, c);
	}
	//得出改变后的前缀和
	for (int i = 1;i <= n;++i)
	{
		for (int j = 1;j <= m;++j)
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
	}
	//打印输出
	for (int i = 1;i <= n;++i)
	{
		for (int j = 1;j <= m;++j)
			printf("%d ", b[i][j]);
		printf("\n");
	}
	return 0;
}

双指针算法

第一类

​ 两个指针分别指向两个序列，例如归并排序

第二类

​ 两个指针都指向一个序列，一个在区间的开头，另一个在区间的结尾,例如快排

双指针算法并非一定要用指针来表示

核心思想

先写出一种暴力做法，然后观察i与j之间是否存在关联，比如单调性，从而优化代码

for(int i = 0;i < n;++i)
	for(int j = 0;j < n;++j)
		if(check(i,j))
		...

将上方原先O（n^2)的朴素算法优化为O（n）

通用模板

for(i = 0,j = 0;i < n; ++i)
{
	//符合条件 j++
	while(j < i && check(i,j)) j++;
	
	//每道题后面的具体逻辑
}

举例

#define _CRT_SECURE_NO_WARNINGS 1
//实现以空格为分隔符换行打印一个带有多个空格的字符串
#include <iostream>
#include <string>
using namespace std;

int main()
{
	string str;//string定义字符串

	getline(cin,str);//读取一行字符串

	int len = str.size();//得到字符串长度

	for (int i = 0;i < len;++i)
	{
		int j = i;
		
		while (j < len && str[j] != ' ') j++;

		//具体逻辑

		for (int k = i;k < j;++k) cout << str[k];
		cout << endl;

		i = j;
	}
}

例题

#define _CRT_SECURE_NO_WARNINGS 1
//求一序列中最长连续子序列的长度
//可以跳数，即2，3，5，但子序列不能有重复元素
#include <iostream>

using namespace std;

const int N = 10010;

int n;
int a[N], s[N];
//a存储序列，s存储每个数字的重复次数

int main()
{
	cin >> n;

	for (int i = 0;i < n;++i) cin >> a[i];

	int res = 0;

	for (int i = 0,j = 0;i < n;++i)
	{
		s[a[i]]++;
		//存储每个数字的重复次数
		
		//运用双指针算法
		while (s[a[i]] > 1)
		{
			//当出现重复数字时，让j追上i
			s[a[j]]--;
			j++;
		}
		res = max(res, i - j + 1);
		//总共计算n次res
	}

	cout << res << endl;

	return 0;
}

例题题解说明：

​ a和s分别作为存储序列和存储每个元素重复次数的数组，

​ 在每次for循环记录每个重复元素次数

​ 如果大于1则利用双指针使得 j 能够追上i，即双指针算法的原理

​ i作为结尾，j作为开头，让j不断自增直到i与j相等

​ **此时 j 就可以作为新子序列的首元素坐标 **

​ 并利用res记录每次的子序列长度

​ 整个题解可以理解为，用res记录子序列的长度，如果不出现重复元素则让res由i-j+1得出，如果出现重复元素，先记录新子序列的长度，再与上一个子序列进行比较，每次遍历都运算一次，时间复杂度就为O（n），最后快速得出最长连续子序列的长度

主要作用

​ 优化运算量，时间复杂度

位运算

​ 最常用的两种操作

1.n的二进制表示中第k位是几

​ 比如

n = 15 的 二进制 （1111）
    从个位起算第0位，十位为第二位，以此类推

操作符>>

把n的第k位移到最后一位

比如

n = 16, k = 3;
n == (0001 0000)
n >> k  == (0010)
n = 15,k = 3
n == (0000 1111)
n >> k == (0000 0001)

2.n的二进制个位是多少

比如

n = 2
n == (0010)
n的个位为0

操作符&

按位与&，两个操作数按位与时，二进制某一位相同则为1，不同则为0

比如

n == 2,k = 1
n == (0010)
k== (0001)
四位都不相同
n&1 ==(0000)

3.进阶运算

​ 计算某数二进制某一位是多少

//计算一个数二进制某一位是多少
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;

int main()
{
	int n,k;//某个数n，哪一位k

	cin >> n>>k;

	cout << ((n >> k) & 1) << endl;

	return 0;
}

lowbit函数

返回n的二进制的最低位1，即返回最后一个是1的数，最后的1之后有多少0就再返回多少个0，再把它转化为十进制数

函数实现

int lowbit(int n)
{
	return n&(-n);
}

或者

int lowbit(int n)
{
	return n&(~n+1)
}

关于按位取反~的解释：按位取反 c语言基础难关：按位取反_涅槃豆的博客-CSDN博客](https://blog.csdn.net/niepandou/article/details/128422923?spm=1001.2014.3001.5501))

原理

n & （-n）  实际上按位与的是他们的补码
n如果为1
n 的 补码为0000 0000
-n的补码为 1111 1110
按位与得到的就是最低位1与其之后的0转化出的十进制数

模板

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;
int my_lowbit(int n)
{
	return n & (-n);
}
int main()
{
	int n;
	cin >> n;
	cout << my_lowbit(n) << endl;
	return 0;
}

运用

//求出一个数二进制中的个数
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

int lowbit(int n)
{
	return n & (-n);
}
int main()
{
	int n;
	cin >> n;

	int res = 0;//计算次数

	while (n)
	{
		n -= lowbit(n);//每次减去n的最后一位1
		res++;
	}
	cout << res << endl;
	return 0;
}

整数离散化

离散化的概念

对一组序列进行升序排列，然后用0映射，代表序列的最小数，1映射第二小的数，以此类推，与利用数组存储相似

如果序列中有重复元素，应当先去重删除重复元素再排序映射

对序列1 2 2 3 5离散化
排序得到1 2 2 3 5
去重并删除得到1 2 3 5
离散化映射
序列1 2 3 5
映射0 1 2 3

模板

int main()
{
	vector<int> alls;//存储将要离散化的数据
	sort(alls.begin(), alls.end());//对所有值排序
    //unique对所有元素去重，重复的元素会被放在最后
	//unique返回值为去重排序后前排未去重元素的总数
	//用erase函数对已放在后排的元素删除
	alls.erase(unique(alls.begin(), alls.end()),alls.end());

例题

1

//寻找序列离散化后特定值对应的映射坐标
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int n,x;
vector<int> alls;//存储将要离散化的数据

int find(int x)
{
	int l = 0, r = alls.size() - 1;
	while (l < r)
	{
		int mid = (l + r) >> 1;
		if (alls[mid] >= x) r = mid;
		else l = mid + 1;
	}
	return r;//映射到0,1,2,3
	//r + 1 映射到1,2,3
}
int main()
{
	cin >> n >> x;

	//输入n个数据
	int number;
	for (int i = 0;i < n;++i)
	{
		cin >> number;
		alls.push_back(number);
	}
	sort(alls.begin(), alls.end());//对所有值排序
	alls.erase(unique(alls.begin(), alls.end()),alls.end());
	//unique对所有元素去重，重复的元素会被放在最后
	//unique返回值为去重排序后前排未去重元素的总数
	//用erase函数对已放在后排的元素删除

	//求出离散化的值
	//二分查找其下标
	cout << find(x) << endl;

	return 0;
}

2

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。

现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c。

接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式

第一行包含两个整数 n 和 m。

接下来 n 行，每行包含两个整数 x 和 c。

再接下来 m 行，每行包含两个整数 l 和 r。

输出格式

共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围

−109≤x≤109,
1≤n,m≤105,
−109≤l≤r≤109,
−10000≤c≤10000

输入样例：

3 3
1 2
3 6
7 5
1 3
4 6
7 8

输出样例：

8
0
5

题解

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;
const int N = 300010;

int n, m;
int a[N], s[N];
vector <int> alls;
vector<PII> add, query;

int find(int x)
{
	int l = 0, r = alls.size() - 1;
	while (l < r)
	{
		int mid = (l + r) >> 1;
		if (alls[mid] >= x) r = mid;
		else l = mid + 1;
	}
	return r + 1;
}
int main()
{
	cin >> n >> m;
	for (int i = 0;i < n;++i)
	{
		int x, c;
		cin >> x >> c;
		add.push_back({ x,c });

		alls.push_back(x);
	}

	for (int i = 0;i < m;++i)
	{
		int l, r;
		cin >> l >> r;
		query.push_back({l,r});

		alls.push_back(l);
		alls.push_back(r);
	}

	//去重

	sort(alls.begin(), alls.end());
	alls.erase(unique(alls.begin(),alls.end()),alls.end());

	//处理插入
	for (auto item : add)
	{
		int x = find(item.first);
		a[x] += item.second;
	}

	//预处理前缀和
	for (int i = 1;i <= alls.size();++i) s[i] = s[i - 1] + a[i];

	// 处理询问
	for (auto item : query)
	{
		int l = find(item.first), r = find(item.second);
		cout << s[r] - s[l - 1] << endl;
	}
	return 0;
}

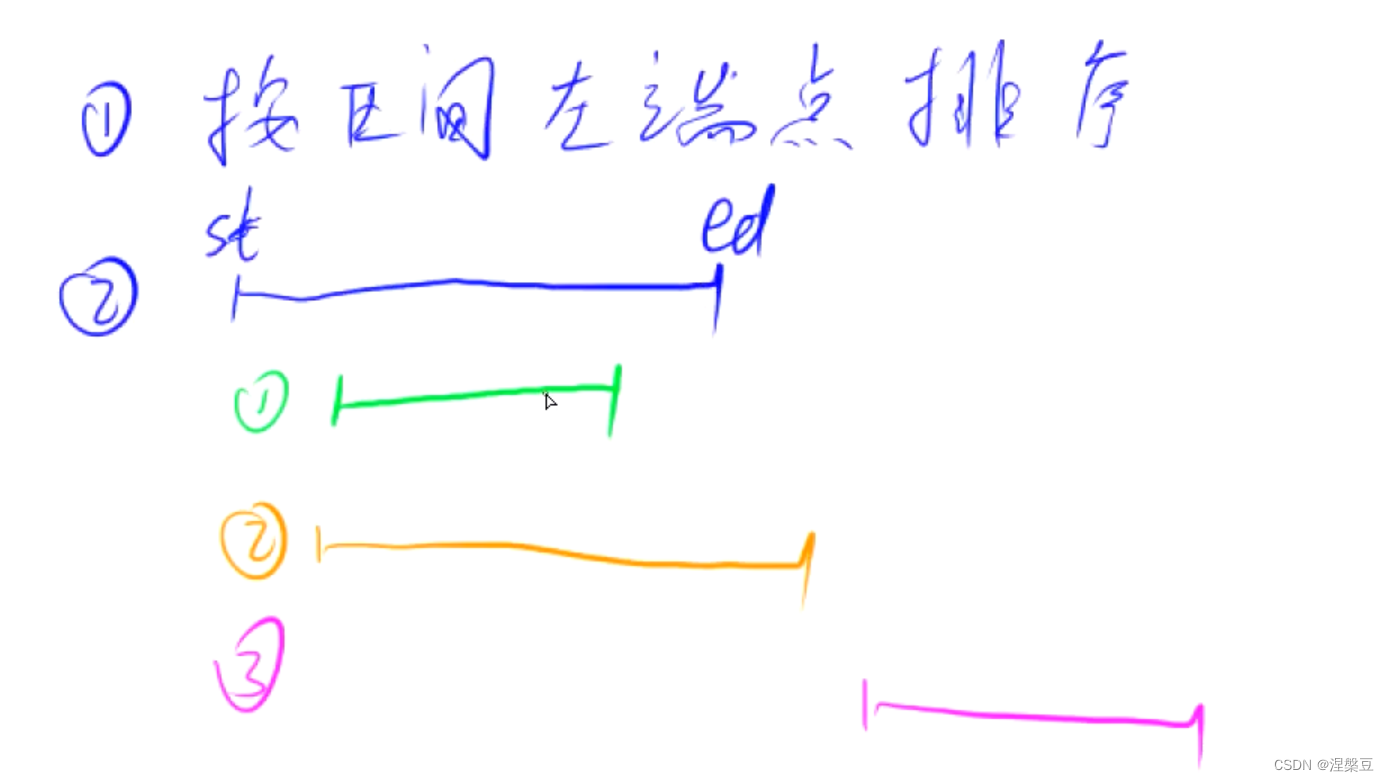
区间合并

​ 概念：在有序升序序列中，如果某一区间合另一区间存在交集，则两个区间可以合并为一个区间

​ 思考情况：

75a73960e38c48879bde94b667d5ff36

1.绿色区间在蓝色区间内部
2.橙色区间与蓝色区间有交集
3.粉色区间与蓝色区间无关联

最终得到新的合并区间[ st , ed ]

st全称start，ed全称end

例题

题目描述
给定 n 个区间 [li , ri]，要求合并所有有交集的区间。
注意如果在端点处相交，也算有交集。
输出合并完成后的区间个数。
例如：[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。

输入格式
第一行包含整数 n。
接下来 n 行，每行包含两个整数 l 和 r。

输出格式
共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围
1 ≤ n ≤ 100000 ,
−1e9 ≤ li ≤ ri ≤ 1e9

输入样例

5
1 2
2 4
5 6
7 8
7 9

输出样例

3

题解

#define _CRT_SECURE_NO_WARNINGS 1
//将所有 有交集的区间合并
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 100010;

int n;
vector<PII> segs;//存储左端点与右端点

void merge(vector<PII>& segs)
{
	vector<PII> res;
	sort(segs.begin(), segs.end());//pair的sort排序优先以左端点排序，左端点相同则看右端点

	int st = -2e9, ed = -2e9;
	for (auto seg : segs)
	{
		if (ed < seg.first)//区间在所维护区间的左端，没有任何区间
		{
			if (ed != -2e9) res.push_back({ st,ed });
			st = seg.first, ed = seg.second;
		}
		else //存在交集
		{
			ed = max(ed, seg.second);
		}
	}
	if (st != -2e9) res.push_back({ st,ed });
	segs = res;
}
int main()
{
	cin >> n;
	for (int i = 0;i < n;++i)
	{
		int l, r;
		cin >> l >> r;
		segs.push_back({ l,r });
	}

	merge(segs);//对区间合并

	cout << segs.size() << endl;//segs的size刚好就是其区间数量
	return 0;
}

数据结构

链表与邻链表

0.传统的链表创建方式在运算速度上非常慢

struct ListNode{
  	int val;
    struct ListNode* next;
};

new struct ListNode();//new一次很慢,因为new是动态分配

1.数组模拟单链表

数组模拟链表，也成为静态链表

链表的实现方式：
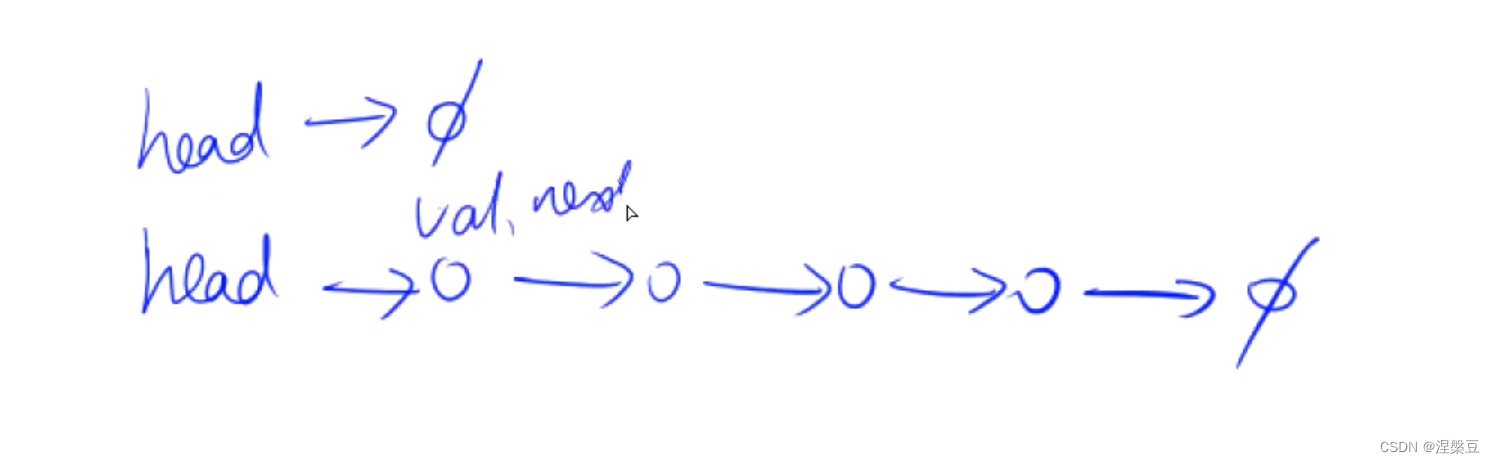
a32c163e3b6545f9b3663d34b6cc5fef

一开始用head指针存储链表头节点，head之后就是空指针

之后让head之后的指针指向新节点，以此类推，直到最后一个节点，再让下一个节点指向空指针

定义e[n]为该节点的值，ne[n]为该节点的next指针

5adf1592306146beac73a8098e29ed0a

e[0] = 3,ne[0] = 1(指节点1)

e[1] = 5,ne[1] = 2(指节点2)

…

e[3] = 9,ne[3] = -1(空节点)

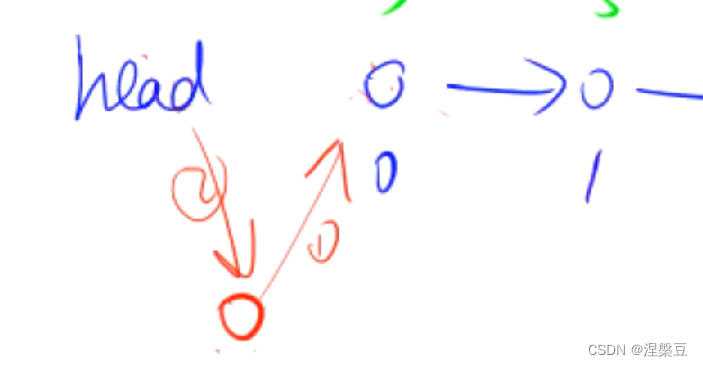
如何在头节点插入一个节点（算法题常用）

链表需要数形结合
48157884963444d88af4026c22a21709

1.将所想要插入的值的next指针指向0节点

2.将head的next指针指向该值

3.存储该值

代码实现

void add_to_head(int &x)//把一个值插入到头节点
{
	ne[idx] = head;//将该值的指针指向head所指的next节点	
	head = idx;//将head指向next节点的指针删掉，改成指向该值的指针
	e[idx] = x;//存储该值
	idx++;//该点已使用过，所以将idx改为下一节点下标
}

如何在任意位置插入一个值

1.首先需要直到该位置的上一节点k

2.与头节点插入类似，先让该值的next变为k的next指针

3.让k的next指针指向该节点

4.存储该值

实现代码

void add(int& k, int& x)//一般插入节点,将x插入到k节点之后
{
	ne[idx] = ne[k];//将该值的next改为k的next
	ne[k] = idx;//k的next指向该值
	e[idx] = x;//存储x
	idx++;
}

如何删除一个节点

链表节点的删除本质上是跳过该节点

实现代码

void remove(int& k)//删除某节点后面的点
{
	ne[k] = ne[ne[k]];//ne[ne[k]]的意思就是该节点的next的next
}

总实现代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

const int N = 100010;

int head, e[N], ne[N];//head头节点，e节点值，ne指next指针
int idx;//存储当前用到哪个节点,下标

void Init()//初始化链表
{
	head = -1;
	idx = 0;
}

void add_to_head(int &x)//把一个值插入到头节点
{
	ne[idx] = head;//将该值的指针指向head所指的next节点	
	head = idx;//将head指向next节点的指针删掉，改成指向该值的指针
	e[idx] = x;//存储改值
	idx++;//该点已使用过，所以将idx改为下一节点下标
}

void add(int& k, int& x)//一般插入节点,将x插入到k节点之后
{
	ne[idx] = ne[k];//将该值的next改为k的next
	ne[k] = idx;//k的next指向该值
	e[idx] = x;//存储x
	idx++;
}

void remove(int& k)//删除某节点后面的点
{
	ne[k] = ne[ne[k]];//ne[ne[k]]的意思就是该节点的next的next
}
int main()
{
	Init();
}

例题

题目描述

实现一个单链表，链表初始为空，支持三种操作：
向链表头插入一个数；
删除第 k个插入的数后面的数；
在第 k个插入的数后插入一个数。
现在要对该链表进行 M次操作，进行完所有操作后，从头到尾输出整个链表。
注意:题目中第 k个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式

第一行包含整数 M，表示操作次数。
接下来 M行，每行包含一个操作命令，操作命令可能为以下几种：

H x，表示向链表头插入一个数 x。
D k，表示删除第 k个插入的数后面的数（当 k 为 0时，表示删除头结点）。
I k x，表示在第 k个插入的数后面插入一个数 x（此操作中 k 均大于 0）。

输出格式

共一行，将整个链表从头到尾输出。
数据范围
1≤M≤10000

题解

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;
const int N = 10010;

int idx, e[N], ne[N];
int head;

void Init()
{
	head = -1;
	idx = 0;
}
void add_to_head(int x)
{
	e[idx] = x;
	ne[idx] = head;
	head = idx;
	idx++;

}

void add(int k, int x)
{
	e[idx] = x;
	ne[idx] = ne[k];
	ne[k] = idx;
	idx++;
}

void remove(int k)
{
	ne[k] = ne[ne[k]];
}
int main()
{
	int m;
	cin >> m;
	Init();
	while (m--)
	{
		char ch;
		int k, x;
		cin >> ch;
		if (ch == 'H')
		{
			cin >> x;
			add_to_head(x);
		}
		else if (ch == 'D')
		{
			cin >> k;
			if (!k) head = ne[head];
			else remove(k-1);
		}
		else
		{
			cin >> k >> x;
			add(k-1, x);
		}
	}

	for (int i = head;i != -1;i = ne[i])
	{
		cout << e[i] << ' ';
	}

	return 0;
}
//10
//H 9
//I 1 1
//D 1
//D 0
//H 6
//I 3 6
//I 4 5
//I 4 5
//I 3 4
//D 6

邻接表：

将每个单链表连接起来，就是邻接表

邻接表的应用：

​ 存储树和图

2.数组模拟双链表

双链表有两个方向，一个指向前，另一个指向后，而单链表只能指向后

因此也可以看出单链表插入时只能插入在往后的方向

需要的数组有e[n],l[n],r[n]和下标idx

e[n]表示该点的值

l[n]表示该点左边节点的指针

r[n]表示右边节点的指针，与单链表next同理

idx表示第几次操作数

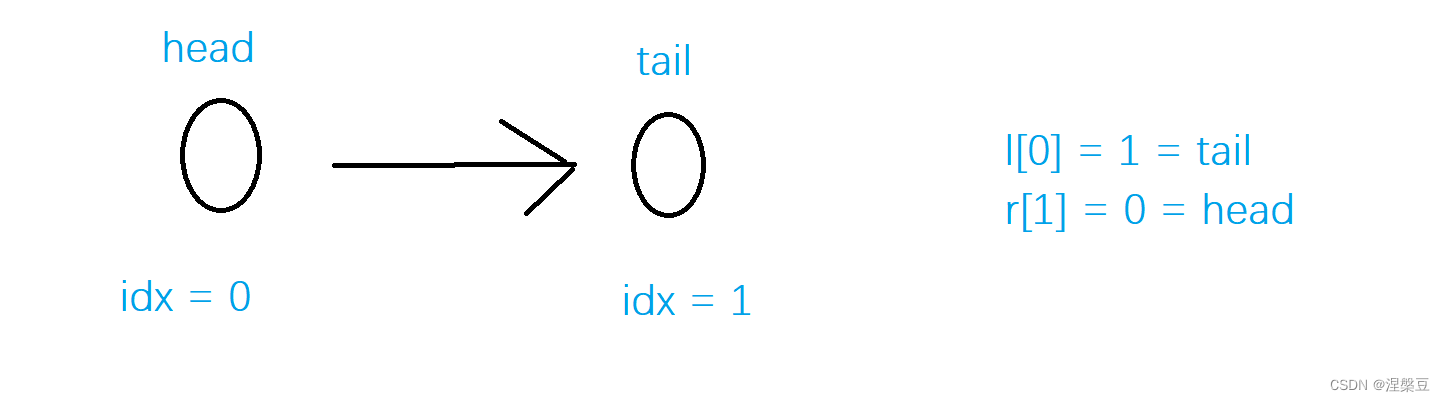
head默认为0，tail默认为1
bd052dd4f7ad45e186f39f4d5166a5eb

对于插入节点和删除节点的操作与单链表相类似

插入节点

1.存储要插入节点的值（可以放在任意位置）

2.改变k的右节点和插入值的左节点，让k和idx连接

3.改变k原先右节点的左节点和插入值的右节点，让k原先的右节点和插入值连接

4.最后操作数+1

实现代码

void addr(int k,int &x)//在k节点的右边插入一个点
{
	e[idx] = x;
	r[idx] = r[k];
	l[idx] = k;
	l[r[k]] = idx;//这两步
	r[k] = idx;//顺序不能变
	idx++;
}

如果想要在k的左边插入一个节点，可以理解为在k的左节点的后面插入一个点，也就是add( l [ k ] , x )

删除节点

让该节点的左节点所指的next直接指向该节点的右节点

让该节点的右节点所指的last直接指向该节点的左节点

实现代码

void remove(int k)//删除第k个节点
{
	r[l[k]] = r[k];
	l[r[k]] = l[k];
}

总实现代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

const int N = 10010;

int e[N], l[N], r[N], idx;

void Init()
{
	r[0] = 1, l[1] = 0;//r[0] = 1表示右端点即tail，l[1] = 0表示左端点即head
	idx = 2;
}
void add(int k,int &x)//在k节点的右边插入一个点
{
	e[idx] = x;
	r[idx] = r[k];
	l[idx] = k;
	l[r[k]] = idx;//这两步
	r[k] = idx;//顺序不能变
	
	idx++;
}

void remove(int k)//删除第k个节点
{
	r[l[k]] = r[k];
	l[r[k]] = l[k];
}
int main()
{
	Init();
}

栈

栈的特点

先进后出，和一个半封闭容器类似，放了一堆肉饼，先放的肉饼后倒出来

stk[n]数组代表栈，tt代表栈点

关于栈的插入

void add(int x)//插入元素
{
	stk[++t] = x;
}

关于栈的删除

void del( )//删除元素，即弹出一个肉饼
{
	tt--;
}

关于判断栈是否为空

bool stkempty()//判断栈是否为空
{
	if (tt > 0) return false;
	else return true;
}

总实现代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

const int N = 10010;

int stk[N], tt;//stk表示栈，tt表示栈点下标

void add(int x)//插入元素
{
	stk[++t] = x;
}

void del( )//删除元素，即弹出一个肉饼
{
	tt--;
}

bool stkempty()//判断栈是否为空
{
	if (tt > 0) return false;
	else return true;
}
//栈顶 stk[tt]
int main()
{
	return 0;
}

例题

问题描述

有一序列，输出每个数左边第一个比他小的数，没有则输出-1

诀窍：在while循环判断条件时，只要想该数不符合条件则跳过即可

//找出每个数左边离它最近的比它大/小的数
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstdio>
using namespace std;

const int N = 10010;

int stk[N], tt;


//暴力法
//void vio(int n)
//{
//	for (int i = 0;i < n;;++i)//对每个数的列举
//	{
//		int j = 0;
//		for (j = i -1;j >= 0;--j)
//		{
//			if (stk[i] > stk[j])
//			{
//				cout << stk[j]<<' ';
//				break;
//			}
//		}
//		if (j == -1) cout << -1 << ' ';
//	}
//}

int main()
{
	int n;
	scanf("%d ", &n);

	//单调栈法
	for (int i = 0;i < n;++i)
	{
		int x;
		scanf("%d ", &x);
		while (tt && stk[tt] >= x) tt--;
		if (tt) printf("%d\n", stk[tt]);
		else printf("-1\n");

		stk[++tt] = x;
	}

}

队列

队列的特点

先进先出，和枪上膛相似，先插进去的子弹先打出来

q[N]表示队列，hh表示对头，tt表示队尾

关于队列的插入

void add(int x)//队尾插入元素
{
	q[++tt] = x;
}

关于队列的删除（弹出）

void del( )//在队头弹出元素
{
	hh++;
}

关于队列的判断是否为空

bool qempty()//判断是否为空
{
	if (hh <= tt) return false;
	else return true;
}

总实现代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

const int N = 10010;

int q[N], hh, tt = -1;//hh表示队头，tt表示队尾 

void add(int x)//队尾插入元素
{
	q[++tt] = x;
}
void del( )//在对头弹出元素
{
	hh++;
}

bool qempty()//判断是否为空
{
	if (hh <= tt) return false;
	else return true;
}

//对头元素q[hh],队尾元素q[tt]
int main()
{
	return 0;
}

例题

//求出一定序列中，滑动窗口里的最小值和最大值
//第一行输出最小值
//第二行输出最大值 
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

const int N = 1000010;

int a[N],q[N],hh,tt;

int main()
{
	int n,k;
	scanf("%d %d", &n,&k);

	hh = 0, tt = -1;
	for (int i = 0;i < n;++i) scanf("%d", &a[i]);

	for (int i = 0;i < n;++i)
	{
		//判断队头是否滑出窗口
		if (hh <= tt && i - k + 1 > q[hh]) hh++;
		//出队
		while (hh <= tt && a[q[tt]] >= a[i]) tt--;//只要队尾比他大
		//就跳出队列，因为之后的滑动窗口都不会选择这个队尾作为输出结果
		q[++tt] = i;//下标入队，从队尾入
        //放在输出前的原因是
		//队列可能一个不剩，那么的数就是最小值
		if (i >= k - 1) printf("%d ", a[q[hh]]);
		
	}
	cout << endl;
	hh = 0, tt = -1;
	for (int i = 0;i < n;++i)
	{
		//判断队头是否滑出窗口
		if (hh <= tt && i - k + 1 > q[hh]) hh++;
		//出队
		while (hh <= tt && a[q[tt]] <= a[i]) tt--;//只要队尾比他大
		//就跳出队列，因为之后的滑动窗口都不会选择这个队尾作为输出结果
		q[++tt] = i;//下标入队，从队尾入
		if (i >= k - 1) printf("%d ", a[q[hh]]);
	}

	cout << endl;

	return 0;
}

大佬您都看完了，不妨点个关注或者点赞收藏一下吧