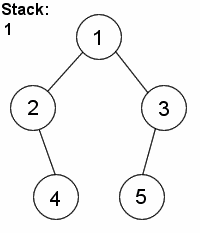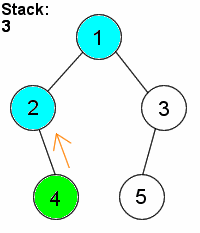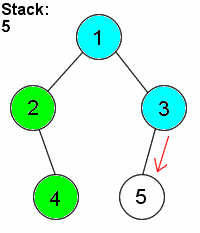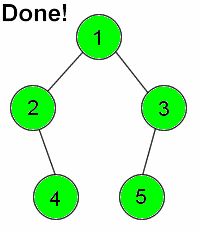
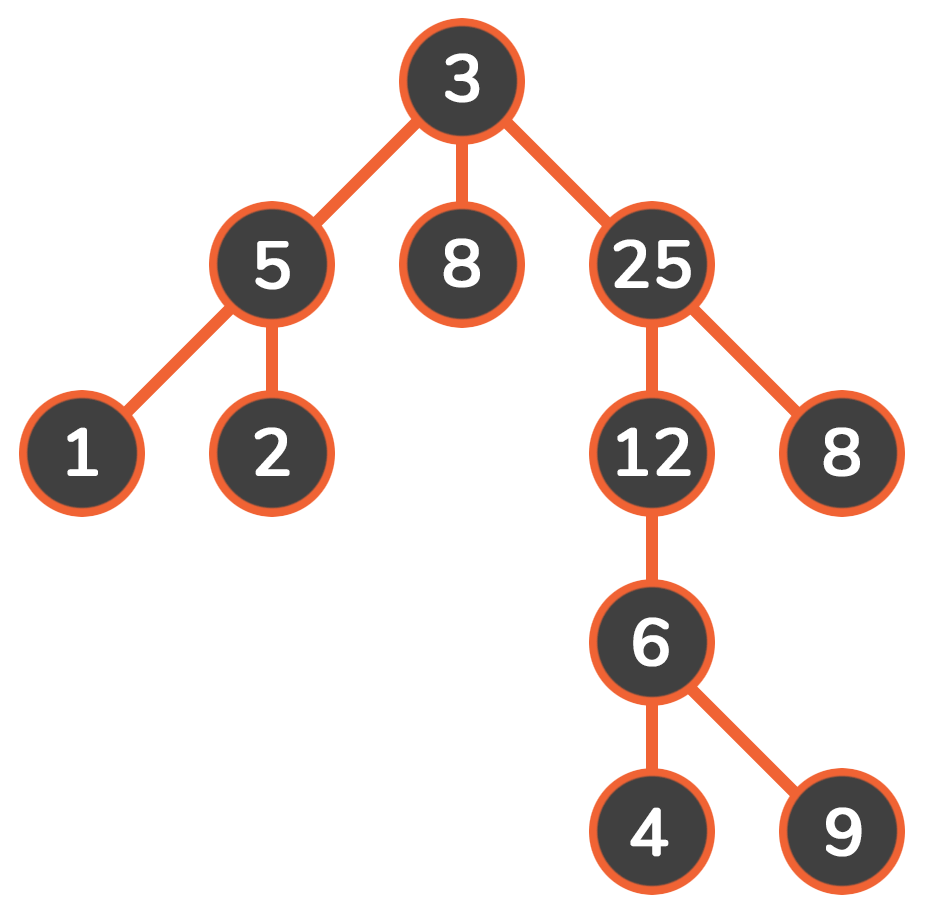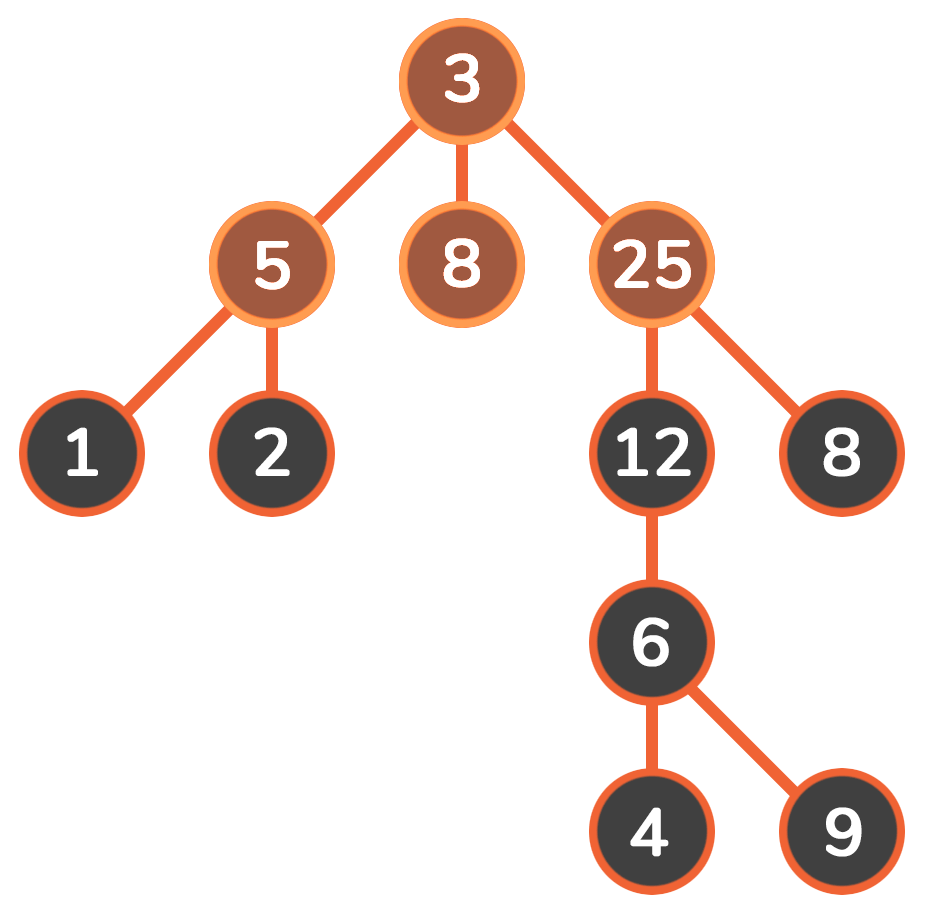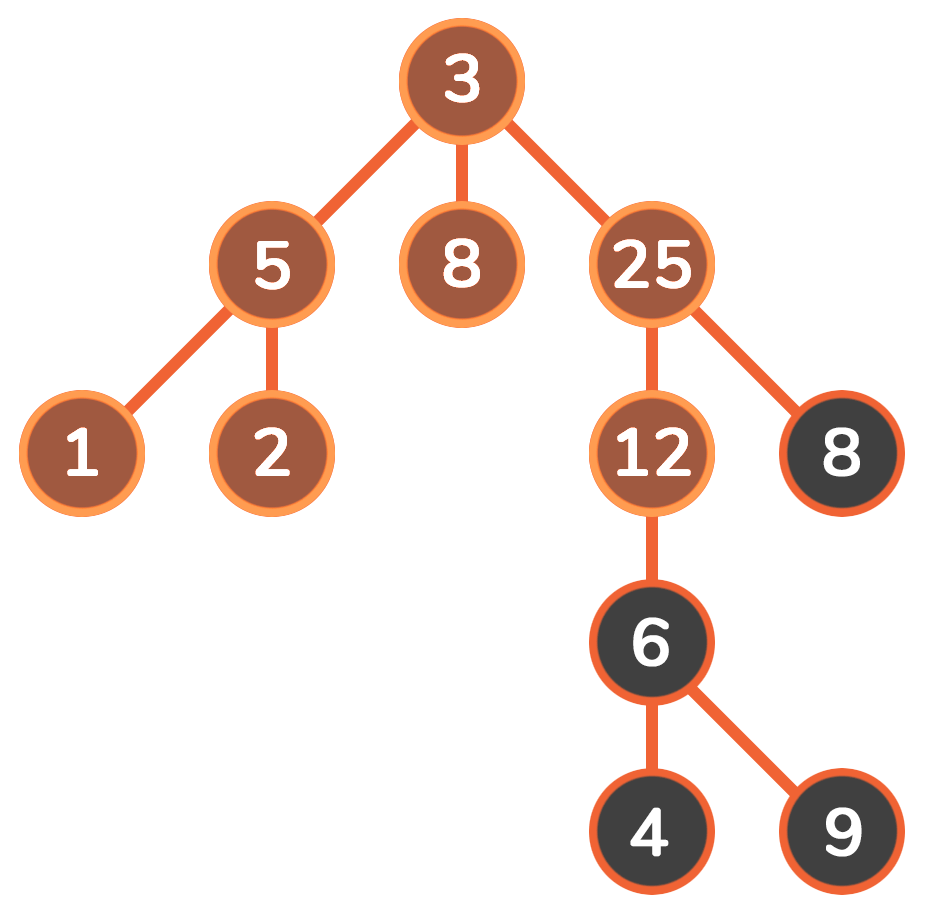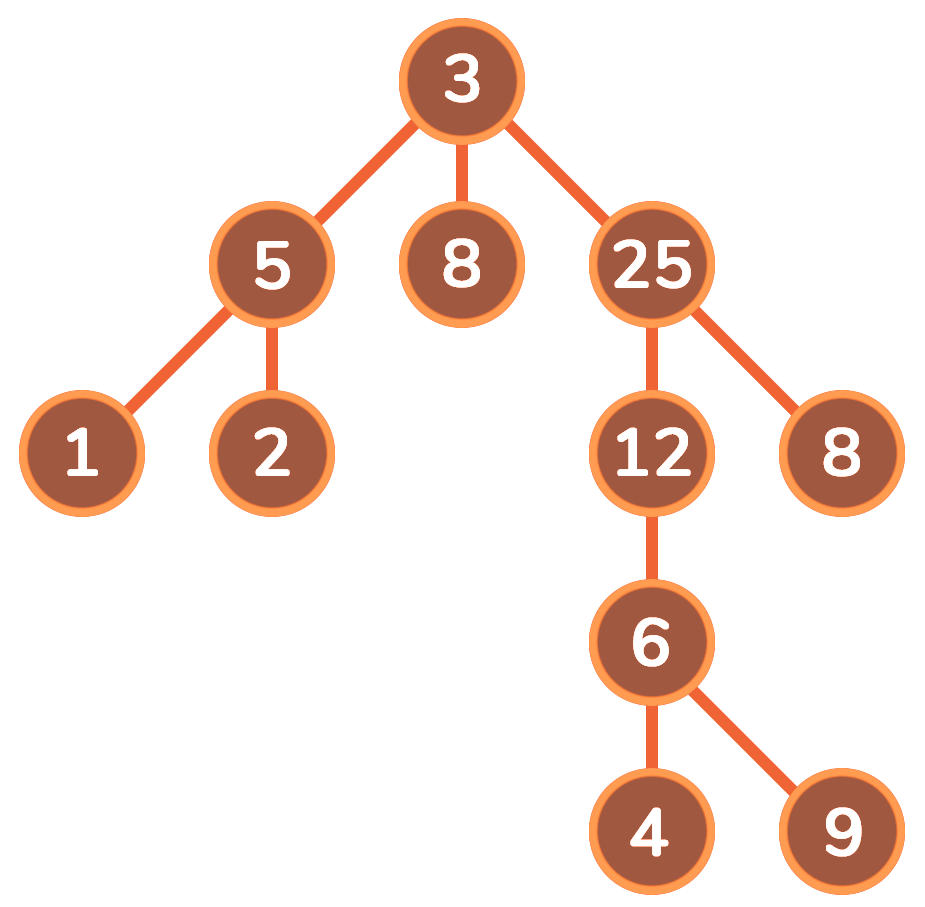
深度优先搜素(dfs) 对二叉树尽可能地往节点的终点搜索,只有走到终点才会返回到分叉路口
特点:执着,不撞南墙不回头
宽度优先搜素(bfs) 对二叉树一层层搜索,只有该层完全搜索完成后才会进行到下一层
特点:稳重,喜欢薅羊毛
对比 从使用的数据结构来看,dfs使用的是栈,bfs使用的是队列
从使用空间看,dfs只需记录这条路径的所有点,空间复杂度为O(h),bfs记录每层的节点,空间复杂度为O(z ^ h),该特点使bfs有了一个最短路的概念
例题 全排列问题(dfs) dfs俗称暴搜,他的关键是顺序
题目描述
按照字典序输出自然数 1 到 n 所有不重复的排列,即 n 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
输入格式
一个整数 n。
输出格式
由 1 - n组成的所有不重复的数字序列,每行一个序列。
每个数字保留 5场宽。
样例 #1
样例输入 #1
样例输出 #1
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
提示
1≤n ≤9。
实现代码 #define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> using namespace std;const int N = 10 ;int n;int path[N];bool st[N];void dfs (int u) if (u == n) { for (int i = 0 ;i < n;++i) printf ("%5d" , path[i]); printf ("\n" ); return ; } for (int i = 1 ;i <= n;++i) { if (!st[i]) { path[u] = i; st[i] = true ; dfs (u + 1 ); st[i] = false ; } } } int main () cin >> n; dfs (0 ); return 0 ; }
n皇后问题 关键:剪枝,即遇到不合理的情况立刻回溯
输入格式
输出格式
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
输出样例:
实现代码 #define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> using namespace std;int n;const int N = 10 ;char g[N][N];bool col[N], dg[N],udg[N];void dfs (int u) if (u == n) { for (int i = 0 ;i < n;++i) printf ("%s\n" , g[i]); return ; } for (int i = 0 ;i < n;++i) { if (!col[i] && dg[u + i] && udg[n - u + i]) { g[u][i] = 'Q' ; col[i] = dg[u + i] = udg[n - u + i] = true ; dfs (u + 1 ); col[i] = dg[u + i] = udg[n - u + i] = false ; } } } int main () cin >> n; for (int i = 0 ; i < n;++i) { for (int j = 0 ;j < n;++j) g[i][j] = '.' ; } }
真全排列 #define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> using namespace std;int a[10 ];bool st[10 ];void dfs (int u) if (u == 10 ) { if (a[1 ] * 100 + a[2 ] * 10 + a[3 ] + a[4 ] * 100 + a[5 ] * 10 + a[6 ] == a[7 ] * 100 + a[8 ] * 10 + a[9 ]) printf ("%d%d%d + %d%d%d = %d%d%d\n" , a[1 ], a[2 ], a[3 ], a[4 ], a[5 ], a[6 ], a[7 ], a[8 ],a[9 ]); return ; } for (int i = 1 ;i <= 9 ;++i) { if (!st[i]) { a[u] = i; st[i] = true ; dfs (u + 1 ); st[i] = false ; } } } int main () dfs (1 ); return 0 ; }
走迷宫(bfs) #include <iostream> #include <queue> #include <cstring> using namespace std;typedef pair<int , int > PII;int n, m;const int N = 101 ;int g[N][N];int d[N][N];queue<PII> q; int bfs () memset (d, -1 , sizeof (d)); d[0 ][0 ] = 0 ; q.push ({ 0 ,0 }); int dx[4 ] = { 1 ,0 ,-1 ,0 }, dy[4 ] = { 0 ,1 ,0 ,-1 }; while (!q.empty ()) { PII t = q.front (); q.pop (); for (int i = 0 ; i < 4 ;++i) { int x = t.first + dx[i], y = t.second + dy[i]; if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1 ) { d[x][y] = d[t.first][t.second] + 1 ; q.push ({x,y}); } } } return d[n - 1 ][m - 1 ]; } int main () cin >> n >> m; for (int i = 0 ;i < n;++i) { for (int j = 0 ;j < m;++j) cin >> g[i][j]; } cout << bfs () << endl; }